---

Most of what are discussed are parts of Algebraic topology (formly called Combinatorial topology)

While I hoped there is a somewhat linear route to understanding things deeply, I think in some places it just makes sense to jump ahead

---

Alert!

The Combinatorial in Combinatorial topology typically refers to the discrete structure of the objects studied, rather than specifically to sets of combinations

---

Motivation for the Simplicial Fraternity or Combinatorial topology

By Simplicial Fraternity I mean the collection of objects that are related to simplices i.e. Simplices, Simplicial complexes, Abstract Simplicial Complexes and Simplicial Sets

Paraphrasing the motivation from ^[4] :

Normal topology studies continuity from an analytical point of view

This view does not have a computational nature: we cannot represent infinite point sets or their associated infinite open sets on a computer.

Combinatorial topology gets us past this limit by examining constructing complicated objects out of simple blocks, and deducing the properties of the constructed objects from the simple blocks.

The simple blocks here being the Simplicial Fraternity

Interesting find:

Introducing the Simplical Approximation Theorem:

Let \( \mathrm{K}, \mathrm{L} \) be simplicial complexes. A simplicial mapping \( f: \mathrm{K} \rightarrow \mathrm{L} \) is called a simpicial approximation of a confinuous function \( F: |\mathrm{K}| \rightarrow |\mathrm{L}| \) if for every point \( x \in |\mathrm{K}|, |f|(x) \) is in the minimal closed simplex of L containing the point \( \mathrm{F}(x)\)

Quoting verbatim from ^[6]

The simplicial approximation theorem is a foundational result for algebraic topology, guaranteeing that continuous mappings can be (by a slight deformation) approximated by ones that are piecewise of the simplest kind. It applies to mappings between spaces that are built up from simplices—that is, finite simplicial complexes. The general continuous mapping between such spaces can be represented approximately by the type of mapping that is (affine-) linear on each simplex into another simplex, at the cost (i) of sufficient barycentric subdivision of the simplices of the domain, and (ii) replacement of the actual mapping by a homotopic one.

---

Simplex

I like the definition given in the book Topology by Klaus Janich ^[1] because among other things it emphasizes the concept of the general position

By a k-dimensional simplex or k-simplex in \( \mathrm{R}^n \) we mean the convex hull \( s(v_o,\ldots, v_k) \) of k + 1 points in the general position

By convex hull of points \(v_0,\ldots,v_k\) we mean \( \bigl\{ \sum_0^k \lambda_i v_i | \lambda_0 + \lambda_1 + \ldots + \lambda_k = 1 \bigr\} \)

and by general position we mean \( v_1 - v_0, \ldots, v_k - v_0 \) are linearly independent

Simplices by themselves are not interesting because they are contractible (echoing what was said in ^[3])

---

Simplicial Complexes

A simplicial complex \(\mathrm{X}\) in \(\mathbb{R}^n \) is a set of simplices in \(\mathbb{R}^n \) such that:

• Every face of a simplex in \(\mathrm{X}\) is also in \(\mathrm{X}\)
• The intersection of any two simplices in \(\mathrm{X}\) is either empty or a common face of both simplices

Motivation : As per ^[5] Simplicial complexes are combinatorial objects that represent topological space

Sometimes the grander vision of the above listed points gets lost and in the book Topology by Klaus Janich the author draws a diagram that describe what the above rules makes impossible

Here's an example of an Simplical Complex

A circle can be given the structure of a simplical complex (up to homeomorphism) in \( \mathbb{R}^n \) where the 0-simplices (vertices) are (0,0), (0,1) and (1,1) and the equations that determine the 1-simplices are \( 0x + y = 1, x + 0y = 1, x + y = 1 \) where \( x,y \in [0,1] \)

A secondary reason for bringing this up is to give you a sense of how cumbersome things can get when writing to write equations to approximate something like a torus in

---

Abstract Simplical Complex

Continuing from above, it is reasonable to think that working with simplicial complexes one while in the course of determining simplices, ensuring that these simplices intersect properly (in accordance with the rules stated above) requires solving equation and hence burdensome

The cure? : more abstraction

For the purpose of (come back here), what is (deemed) important is the count of the simplices there are and which faces they are glued along. This is what we call combinatorial (discrete) information

To sum up the sentiment succintly: It is often easier to construct a complex abstractly and to worry abut how to put it into Euclidean space later.

Before we go on to a proper definition, we need to establish the concept of a k-skeleton

The k-skeleton of a simplicial complex is the collection of all simplices of dimension at most k and is denoted by \( X^k \)

The definition of an abstract simplicial complex is as follows: (nicked from Greg Friedman's paper on Simplicial Sets)

Definition 2.2. An abstract simplicial complex consists of a set of “vertices” \(\mathbf{X}^0\) together with, for each integer k, a set \(\mathbf{X}^k\) consisting of subsets of \(\mathbf{X}^0\) of cardinality k + 1. These must satisfy the condition that any (j + 1)-element subset of an element of \(\mathbf{X}^k\) is an element of \(\mathbf{X}^j\) .

An example of this: consider a Simplicial Complex that resembles an octahedron that is supposed to approximate a sphere ( \(\mathbb{S}^2\))

The Abstract Simplicial Complex (representation) would be something like this

Vertices : \( \{v_0, v_1, v_2, v_3, v_4, v_5\} \)

In terms of k-Skeletons:

\( X^0 = \{\{v_0\}, \{v_1\}, \{v_2\}, \{v_3\}, \{v_4\}, \{v_5\}\} \) , \( X^1 = \{ \{v_0, v_1\}, \{v_0, v_2\}, \{v_0, v_3\}, \{v_0, v_4\}, \{v_5, v_1\}, \{v_5, v_2\}, \{v_5, v_3\}, \{v_5, v_4\}, \{v_1, v_2\}, \{v_2, v_3\}, \{v_3, v_4\}, \{v_4, v_1\} \} \) , \( X^2 = \{ \{v_1,v_5,v_4\}, \{ v_1, v_5, v_2\}, \{ v_2, v_5, v_3\}, \{ v_3, v_5, v_4\}, \{v_1, v_0, v_2\}, \{ v_2, v_0, v_3\}, \{v_3, v_0, v_4\}, \{v_4, v_0, v_1\} \} \)

All in all: \( X = X^0 \cup X^1 \cup X^2 \)

---

Ordered Simplical Complexes

The point of all of this i.e Simplex, Simplicial Complexes and Abstract Simplicial Complexes is to approximate a topological space

The stuff covered so far do an okay job but so far we're not quite there yet. We now look at product operations on simplicial complexes

Why? Product spaces are defined for topological spaces and we want to use an analogous operation for simplicial complexes. Easier said than done

Among other yet to see obstacles, one of the first things we need to do is to define a product of simplicial complexes

Brief bit on the Universal property of Products

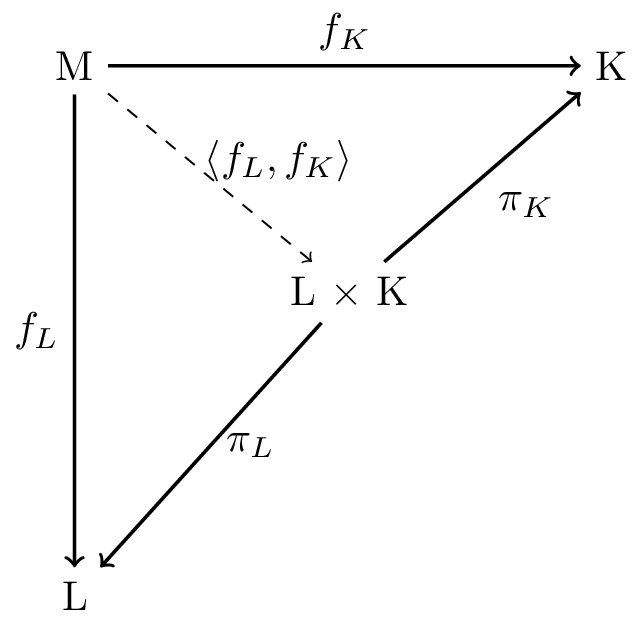
Nicked from ^[4], formalizing the concept of a product from annals of Category Theory

Definition 3.71 Let \(\beth\) be a category and \(L,K\) be objects in \(\beth\). A product of \(L\) and \(K\) is an object, denoted \(L \times K\), together with morphisms \(\pi_L: L \times K \rightarrow L\) and \(\pi_K: L \times K \rightarrow K\) such that forall objects \( M\) together with morphisms \(f_L: M \rightarrow K\) and \(f_K: M \rightarrow K\), there exists a unique morphism \(M \rightarrow L \times K \) denoted \( \left< f_L,f_K \right> \), for which the above diagram commutes

While I'm still grappling with the whole implications of this (maybe I'm overcomplicating things) but this doesn't define the exact computation of the product but tells you whatever you define as the project as long as your have these projections defined along with it, forall

As given in ^[3] the product of two simplicial complexes that follows the universal property of products is :

\( \begin{aligned} V_{K \times L} &= V_K \times V_L \\ S_{K \times L} &= \bigl\{ \sigma \in \mathcal{P}(V_{K \times L}), \pi_L(\sigma) \in S_L \land \pi_K(\sigma) \in S_K \bigr\} \end{aligned} \)

(Again from ^[3]) as an example let us look at the product of a 1-simplex and two 0-simplices

\( \begin{aligned} V_L &= \{V_0, V_1\} \\ S_L &= \{ \{ V_0 \}, \{ V_1 \}, \{ V_0, V_1 \} \} \\ V_K &= \{V_2, V_3\} \\ S_K &= \{ \{ V_2 \}, \{ V_3 \} \} \end{aligned} \)

\( \begin{aligned} V_{K \times L} &= \{ (V_2, V_0), (V_2, V_1), (V_3, V_0), (V_3, V_1) \} \\ S_{K \times L} &= \{ \{(V_2, V_0)\}, \{(V_2, V_1)\}, \{(V_3, V_0)\}, \{(V_3, V_1)\}, \{ (V_2, V_0) , (V_2, V_1) \}, \{ (V_3, V_0) , (V_3, V_1) \} \} \end{aligned} \)

Remember! while \( \mathcal{P}(V_{K \times L}) \) is a lot bigger set than the one above, past the filters in the form of the projection related clauses (i.e. \( \ldots \pi_L(\sigma) \in S_L \land \pi_K(\sigma) \in S_K \bigr\} \)), it gets reduced to the set above

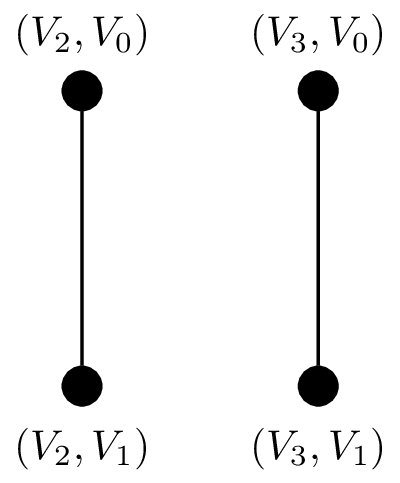
The calculated

But let us look at another example where the geometric intuition of what the product should like does not match the calculated product

Consider the product of two 1-simplices

\( \begin{aligned} V_L &= \{V_0, V_1\} \\ S_L &= \{ \{ V_0 \}, \{ V_1 \}, \{ V_0, V_1 \} \} \\ V_K &= \{V_2, V_3\} \\ S_K &= \{ \{ V_2 \}, \{ V_3 \}, \{ V_2, V_3 \} \} \end{aligned} \)

(I'll be switching to just numbers rather than \(V_i\) for the sake of brevity)

\( \begin{aligned} V_{K \times L} &= \{ (2,0), (2,1), (3,0), (3,1) \} \\ S_{K \times L} &= \{ \{ (2,0) \}, \{ (2,1) \}, \{ (3,0) \}, \{ (3,1) \} \} \cup \{ \{ (2,0), (2,1) \}, \{ (2,0), (3,0) \}, \{ (2,0), (3,1) \}, \{ (2,1), (3,0) \}, \{ (2,1), (3,1) \}, \{ (3,0), (3,1) \} \} \\ & \cup \{ \{ (2,0), (2,1), (3,0) \}, \{ (2,0), (2,1), (3,1) \}, \{ (2,0), (3,0), (3,1) \}, \{ (2,1), (3,0), (3,1) \} \} \cup \{ \{ (2,0), (2,1), (3,0), (3,1) \} \} \end{aligned} \)

(Notice that nothing was filtered out by the projection clauses)

The product calculated here is a 3-simplex

The geometric intuition which assuming we calculated the product with the geometric realization i.e the cartesian product of the simplices would be a square

Soooo what might the fix be? Answer: TOTALLLL ORDERING on simplices and place the total ordering constraint within our definition of a product

i.e \( S_{K \times L} = \{ \sigma \in \mathcal{P}(V_{K \times L}), \pi_L(\sigma) \in S_L \land \pi_K(\sigma) \in S_K \land \pi_L(\sigma) \leq \pi_K(\sigma) \} \)

so going back to the product of two 1-simplices

\( \begin{aligned} V_{K \times L} &= \{ (2,0), (2,1), (3,0), (3,1) \} \\ S_{K \times L} &= \{ \{ (2,0) \}, \{ (2,1) \}, \{ (3,0) \}, \{ (3,1) \} \} \cup \{ \{ (2,0), (2,1) \}, \{ (2,0), (3,0) \}, \{ (2,0), (3,1) \}, \{ (2,1), (3,1) \}, \{ (3,0), (3,1) \} \} \cup \{ \{ (2,0), (2,1), (3,1) \}, \{ (2,0), (3,0), (3,1) \}, \} \end{aligned} \)

---

Quotient-spaces and Quotient Maps: Path to Simplicial Sets

Again nicked from ^[3]

We look at the example of trying to triangulate a \( \mathbb{S}^1 \)

We do this by looking at the circle as a quotient space of the interval \( [0,1] \), and attempting the same with an ordered simplicial complex

The 1-simplex represented by a 1-simplex with representation:

\( V = \{0,1\} \) and \( S = \{ \{0\}, \{1\}, \{0,1\} \} \)

But when the ends are identified, how would you represent this in terms of simplices? It's clearly not a 1-simplex and definitely not a 0-simplex

Could you do this: \( V = \{0,1\} \) and \( S = \{ \{0\}, \{\{1\}\}, \{0,1\}, \{1,0\} \} \) ?

Nope, that doesn't cature the fact that the ends are identified

What about this: \( V = \{0,1\} \) and \( S_0 = \{ \{1\} \} , S_1 = \{ \{0\} \} \) ?

It encodes the information but gives us no indication of where the ends are identified. What if there were explicit functions that show the identification?

\( \begin{aligned} V &= \{0,1\} \\ S_0 &= \{ \{1\} \} , S_1 = \{ \{0\} \} \\ f_0&: S_1 \rightarrow S_0 \text{ where } f_0(1) = 0 \\ f_1&: S_1 \rightarrow S_0 \text{ where } f_1(0) = 1 \end{aligned} \)

---

Simplical sets: The non-categorical version

---

Category Theory Basics

I'm pretty sure there are other pieces that do this justice

---

Category Theory formulation of Simplical Sets